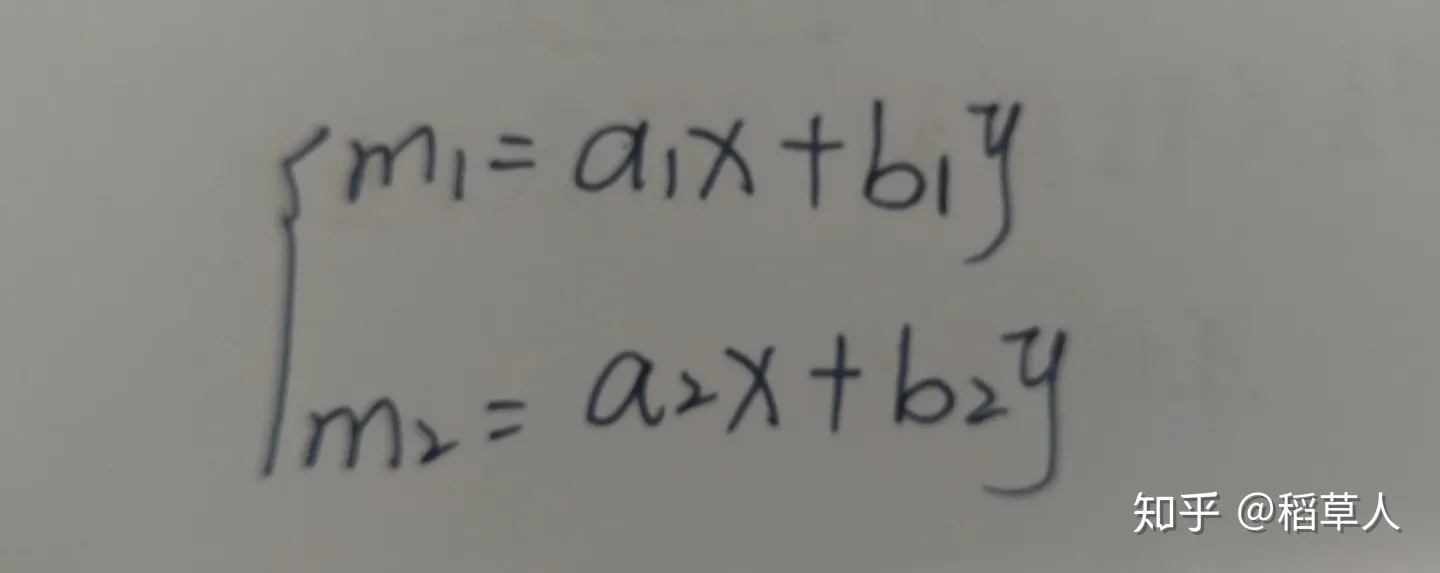搜索到
71
篇与
的结果
-

-

-
 鉴定网络热门数学谣言(借助ChatGPT) ChatGPT比知乎上故作玄虚的一众答主强太多了。之前我一直想不明白为什么所有自然数之和为-1/12。用小学数学的知识简单推算一下已知: {x} 所有自然数为正整数 {x} 两正数之和必定为正数 {x} 加法具有结合律和交换律结论: { }所有自然数之和必为正数一直想不明白哪里来的-1/12逻辑三段论,或者自然数之和为-1/12的推导过程肯定有一个出了问题。知乎上一众答主使用各种奇技淫巧论证了自然数之和为-1/12,却都没有解释为何与已有的数学架构冲突。今天又看到这个暴论,迷惑之际寻求ChatGPT,他的回答的非常完整和严谨。ChatGPT首先给出了一个:“直接的回答”。当我问及这一暴论时,ChatGPT回复这个说法源于一种数学方法的误用。在非常特定的数学和物理上下文中,我们可以使用ζ函数的解析延拓,但在日常生活中,这个结果并没有什么意义。豁然开朗
鉴定网络热门数学谣言(借助ChatGPT) ChatGPT比知乎上故作玄虚的一众答主强太多了。之前我一直想不明白为什么所有自然数之和为-1/12。用小学数学的知识简单推算一下已知: {x} 所有自然数为正整数 {x} 两正数之和必定为正数 {x} 加法具有结合律和交换律结论: { }所有自然数之和必为正数一直想不明白哪里来的-1/12逻辑三段论,或者自然数之和为-1/12的推导过程肯定有一个出了问题。知乎上一众答主使用各种奇技淫巧论证了自然数之和为-1/12,却都没有解释为何与已有的数学架构冲突。今天又看到这个暴论,迷惑之际寻求ChatGPT,他的回答的非常完整和严谨。ChatGPT首先给出了一个:“直接的回答”。当我问及这一暴论时,ChatGPT回复这个说法源于一种数学方法的误用。在非常特定的数学和物理上下文中,我们可以使用ζ函数的解析延拓,但在日常生活中,这个结果并没有什么意义。豁然开朗 -
 Fail2Ban安装使用 安装install fail2bancp /etc/fail2ban/jail.conf /etc/fail2ban/jail.local #将默认配置文件模板复制为正式使用的配置文件nano /etc/fail2ban/jail.local #修改规则在对应的模板后添加enable[sshd]enabled = truesystemctl restart fail2ban.serviceiptables -L #验证 Fail2Ban iptables 规则fail2ban-client status #查看被ban的列表fail2ban-client set ssh unbanip 192.168.1.115 #删除被ban的ip引用自 详细信息请参阅上方链接。 注意Fail2Ban可能与MobaXterm的文件功能冲突,用MobaXterm时关掉f2b
Fail2Ban安装使用 安装install fail2bancp /etc/fail2ban/jail.conf /etc/fail2ban/jail.local #将默认配置文件模板复制为正式使用的配置文件nano /etc/fail2ban/jail.local #修改规则在对应的模板后添加enable[sshd]enabled = truesystemctl restart fail2ban.serviceiptables -L #验证 Fail2Ban iptables 规则fail2ban-client status #查看被ban的列表fail2ban-client set ssh unbanip 192.168.1.115 #删除被ban的ip引用自 详细信息请参阅上方链接。 注意Fail2Ban可能与MobaXterm的文件功能冲突,用MobaXterm时关掉f2b -
 矩阵与行列式的意义(简述) 首先要明白矩阵和行列式概念的提出是因为什么在解一元一次方程时,很容易就根据运算律算出未知数的值而当解二元或是多元方程时,则需要用到换元为了方便计算,将相同变量排成一列便得到了一组有规律的多元方程这组方程有相同个数的变量。因为排列有规律,为了计算方便,便将方程的系数提出,作为一个矩阵放在左边,再将方程的变量提出,作为一个向量放在右边,向量的长度(变量的个数为i)。因为有些方程可能有多个解,当向量中的变量用j个解带入时,便形成了i行j列的矩阵。由此,数学意义便清晰可见了。两个矩阵相乘,左边的矩阵作为系数,右边的矩阵作为多个可能的解。求出的矩阵便是i行(变量数),j列(变量的解数)的矩阵以上是矩阵的数学意义矩阵的几何意义可以用于降维将源坐标系的点通过变换映射到新的坐标系。
矩阵与行列式的意义(简述) 首先要明白矩阵和行列式概念的提出是因为什么在解一元一次方程时,很容易就根据运算律算出未知数的值而当解二元或是多元方程时,则需要用到换元为了方便计算,将相同变量排成一列便得到了一组有规律的多元方程这组方程有相同个数的变量。因为排列有规律,为了计算方便,便将方程的系数提出,作为一个矩阵放在左边,再将方程的变量提出,作为一个向量放在右边,向量的长度(变量的个数为i)。因为有些方程可能有多个解,当向量中的变量用j个解带入时,便形成了i行j列的矩阵。由此,数学意义便清晰可见了。两个矩阵相乘,左边的矩阵作为系数,右边的矩阵作为多个可能的解。求出的矩阵便是i行(变量数),j列(变量的解数)的矩阵以上是矩阵的数学意义矩阵的几何意义可以用于降维将源坐标系的点通过变换映射到新的坐标系。