首先要明白矩阵和行列式概念的提出是因为什么
在解一元一次方程时,很容易就根据运算律算出未知数的值
而当解二元或是多元方程时,则需要用到换元
为了方便计算,将相同变量排成一列便得到了一组有规律的多元方程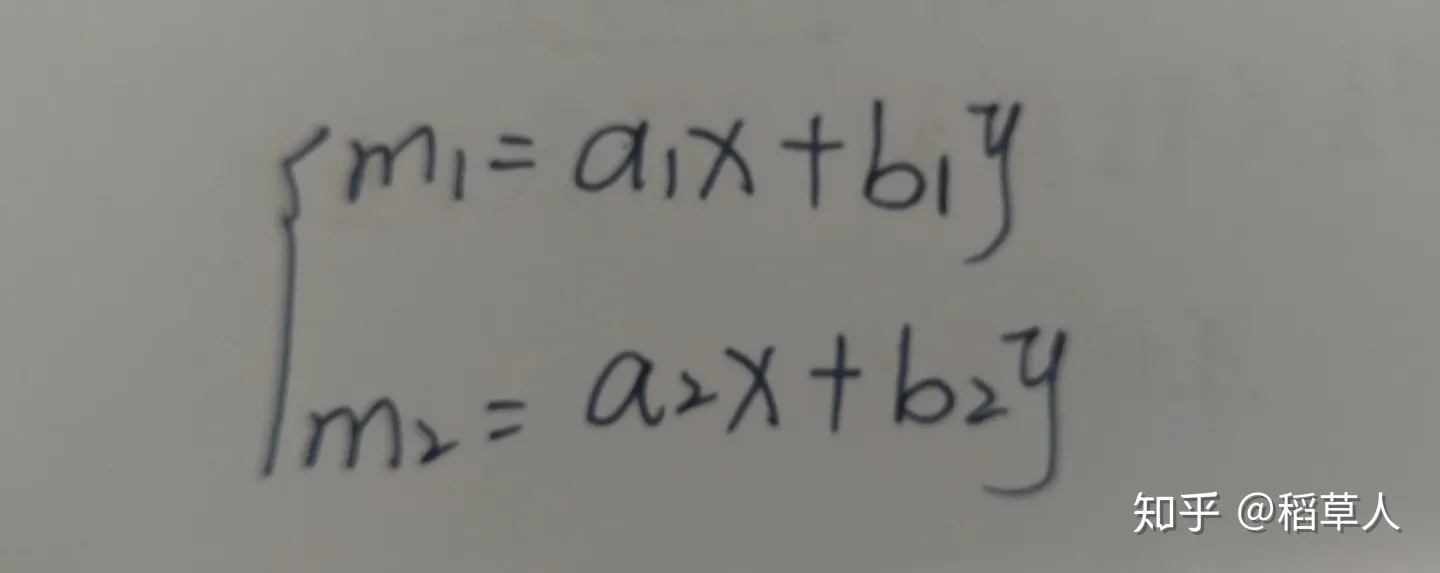
这组方程有相同个数的变量。
因为排列有规律,为了计算方便,便将方程的系数提出,作为一个矩阵放在左边,再将方程的变量提出,作为一个向量放在右边,向量的长度(变量的个数为i)。
因为有些方程可能有多个解,当向量中的变量用j个解带入时,便形成了i行j列的矩阵。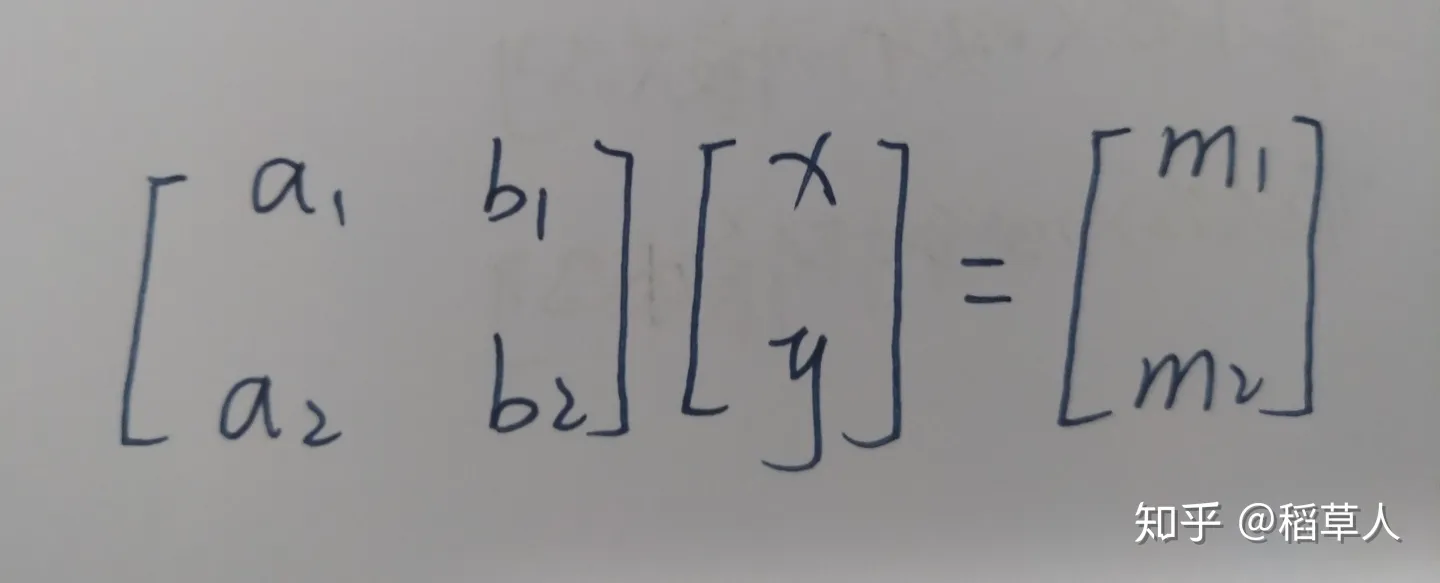
由此,数学意义便清晰可见了。
两个矩阵相乘,左边的矩阵作为系数,右边的矩阵作为多个可能的解。求出的矩阵便是i行(变量数),j列(变量的解数)的矩阵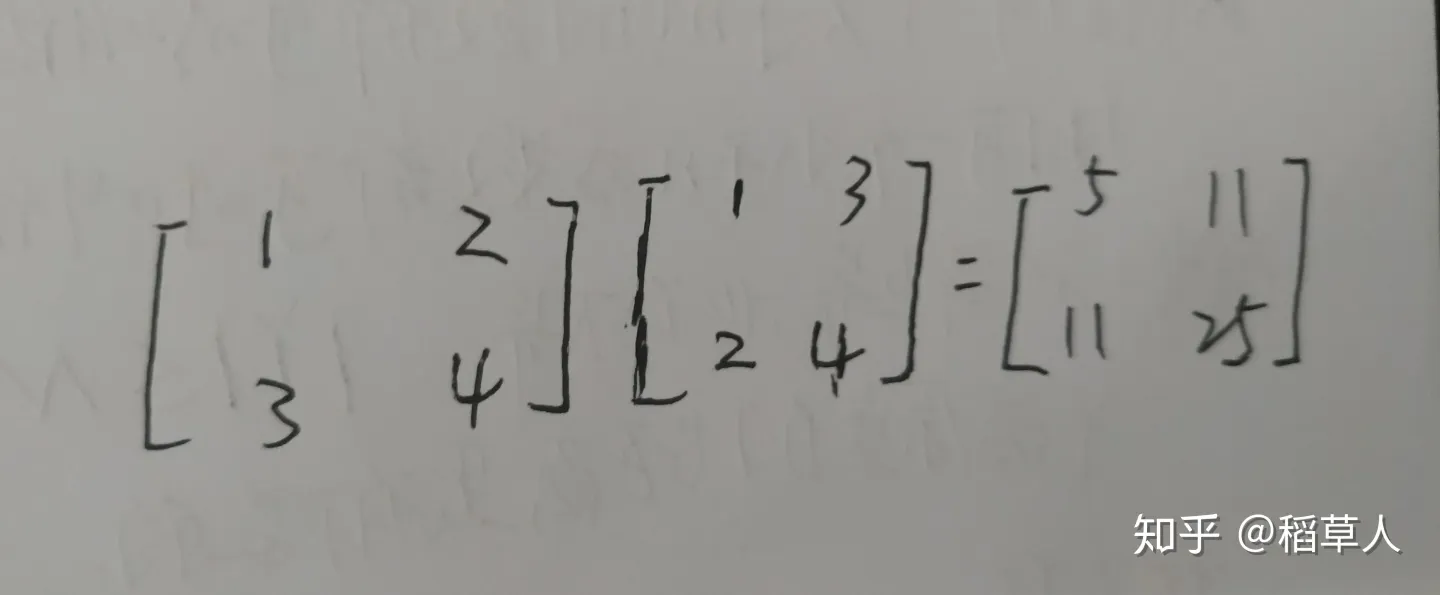
以上是矩阵的数学意义
矩阵的几何意义
可以用于降维
将源坐标系的点通过变换映射到新的坐标系。
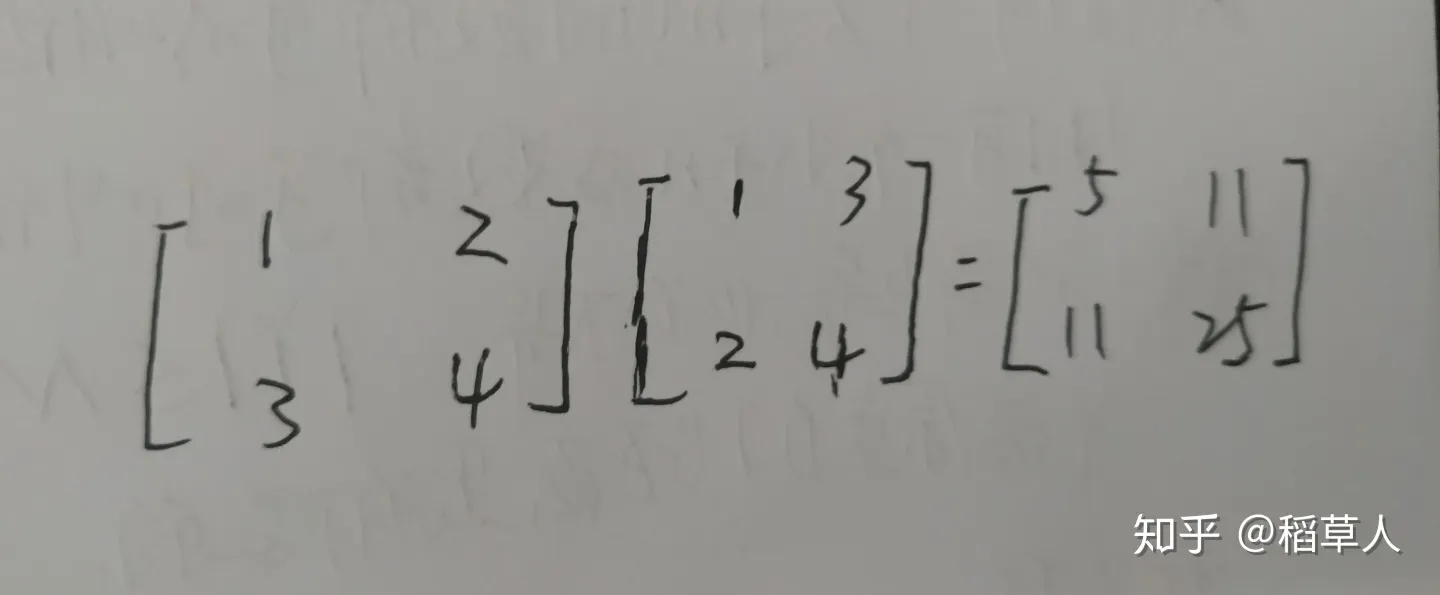




评论 (0)